Лазерная дифракция

Принцип работы лазерных анализаторов размера частиц Wintrac основанных на методе лазерной дифракции.

Лазерный гранулометр Wintrac представляет собой оптический анализатор, предназначенный для определения размеров частиц в жидких дисперсных системах и определения гранулометрического состава сыпучих порошков.

Принцип работы оптического анализатора размеров частиц основан на методе статического светорассеяния и лазерной дифракции.

Лазерные дифрактометры Wintrac 3000 и Wintrac 2000 представляют собой системный блок с интегрированными в него лазерными источниками света, фотодетектирующей системой и кюветным отделением. В системный блок анализатора интегрирован рециркуляционный модуль, являющийся составной частью всей аналитической системы. Все элементы, необходимые для анализа размеров частиц интегрированы в конструкцию анализатора, за исключением компрессора для подачи сжатого воздуха и вакуумного пылеуловителя, применяемых в процессе анализа сухих порошков. Для измерений сухих порошков применяется система пневматического турбулентного диспергирования с регулируемой скоростью дозирования.

В качестве источников когерентного монохроматического излучения (лазерных пучков) используются 2 полупроводниковых лазера.  

Управление лазерным анализатором размеров частиц осуществляется через персональный компьютер с помощью специализированного программного обеспечения Wintrac с интегрированным функционалом для обработки результатов. 

Анализ размера частиц от 0.1 мкм до 8.75 мм

За последние 30 лет лазерная дифракция превратилась в самый распространенный метод анализа размера частиц для всех видов аэрозолей, суспензий, эмульсий и спреев как в лабораторных, так и в производственных условиях.

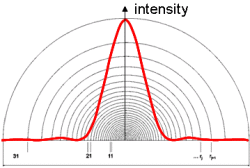
Дифракция лазерного луча – это результат интерференции света на частицах, что математически может быть описано Теорией Фраунгофера или Ми. Для отдельной сферической частицы дифракционная картина имеет типичную круговую структуру. Расстояние r0 от первого минимума до центра зависит от размера частицы, как это показано на рис.1 и 2. Поглощение распределения интенсивности отраженного света происходит при помощи мульти-элементного фотодетектора, как это показано на рис.3.

рис1. Дифракционная картина маленькой частицы	рис.2 дифракционная картина большой частицы	рис.3  Интенсивность распределения от маленькой частицы, зафиксированная полукруглым фотодетектором

Одновременная дифракция более чем одной частицы приводит к суперпозиции дифракционнных картин индивидуальных частиц, в то время как частицы движутся, а дифракция между ними усредняется.

Что такое частица?

На первый взгляд кажется, что вопрос элементарный. Однако понимание этого вопроса, является основой понимания результатов, получаемых различными методами анализа размеров частиц. Процессы диспергирования и форма частиц разных материалов делают процесс анализа размеров частиц, более комплексным вопросом, чем это кажется на первый взгляд.

 

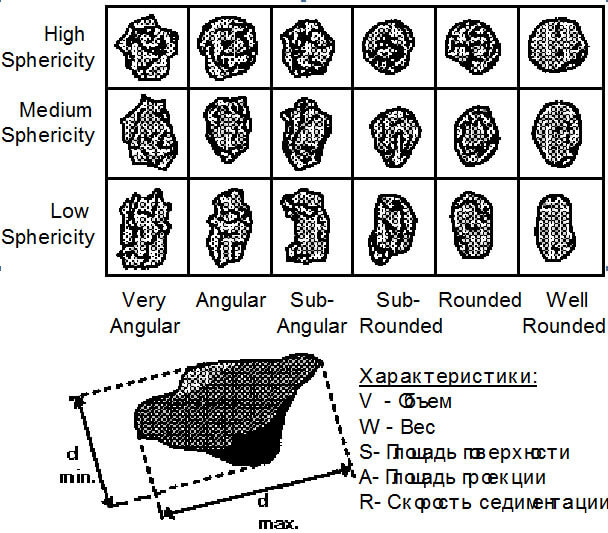
Рисунок 1

Загадка размера частиц.

Представьте, Вам дали линейку и коробок спичек и просят определить размер коробка. Вы можете ответить, что его размеры 20х10х5мм. Вы не сможете выразить эти величины одним числовым значением и сказать, что его размер, например 20мм, т.к. это только одно из значений, определяющее длину коробка. Итак, невозможно выразить длину, высоту и ширину одним числовым значением. Очевидно, что при определении размеров, например песчинки или частицы пигмента, находящегося в емкости с краской, задача еще больше усложняется.

Очевидно, что начальник лаборатории и ОТК заинтересован в получении  

такого единственного числового значения, которое будет максимально полно характеризовать интересующие его частицы. Т.е. фактически, он должен знать увеличился или уменьшился средний размер частиц с момента, например, выпуска последней партии продукции. Это и является основой проблемы измерения размеров частиц - т.е. как выразить одним числовым значением размер частицы, которая имеет несколько величин характеризующих ее размер?

На рисунке 1 показаны несколько зерен песка. Какого они размера?

Эквивалентная сфера.

Единственная форма объекта, который может быть описан одним числовым значением это сфера. Достаточно сказать, что диаметр сферы 50мкм, и это даст исчерпывающую информацию о ее размерах. Охарактеризовать куб таким же образом невозможно, т.к. значение 50мкм может относиться и к длине ребра, и к диагонали.

Но, несмотря на сказанное выше, мы можем в нашем примере с коробком, выразить его размер одним числовым значением. Возьмем такое значение как вес, который как объем, и площадь поверхности является универсальным числовым значением, характеризующим объект. Итак, если у нас есть инструментарий для определения веса коробка, то полученное значение веса мы можем преобразовать значение веса в вес сферы, вспомнив что:

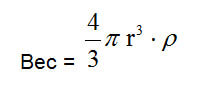
Таким образом, мы получили одно универсальное число (2r) для диаметра сферы, которая имеет такой же вес, как вес нашего коробка. Это теория эквивалентной сферы. Измеряя некоторые характеристики частицы, предполагаем, что они относятся к сфере, рассчитываем универсальное число (диаметр этой сферы), которое характеризует нашу частицу. Этот пример наглядно подтверждает, что нет необходимости описывать размер частицы тремя или более числовыми значениями, которые конечно, более точно выражают размер, но неудобны по многим соображениям для контроля и управления производственными процессами.

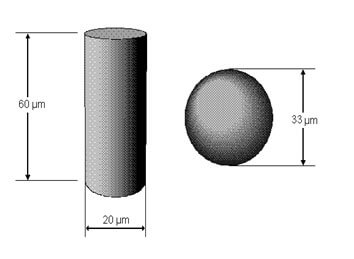
Рисунок 2

Можно заметить, что применение этой теории приводит к проявлению некоторых интересных эффектов, зависящих от формы объекта. Это наглядно иллюстрируется примером цилиндра и эквивалентной ему сферы (рис.2). Однако если цилиндр меняет форму или размер - обязательно меняется объем/вес и выразить эти изменения  (т.е. увеличился цилиндр или уменьшился) можно только через модель  эквивалентной сферы.

Диаметр сферы эквивалентной цилиндру с размерами 100х20мм.

Представьте цилиндр диаметр которого D1=20мкм (т.е. r=10мкм), а высота 100мкм. Сфера с диаметром D2 эквивалентна цилиндру по объему. Диаметр такой сферы можно рассчитать следующим образом:

Объем цилиндра =

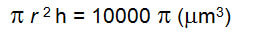
Объем сферы =

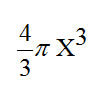
Где Х это радиус сферы с эквивалентным объёмом.

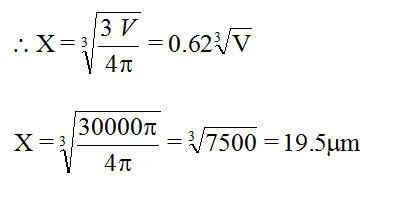
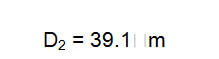
Диаметр сферы, эквивалентной по объему нашему цилиндру с высотой 100мкм и диаметром 20мкм, составляет около 40мкм.

В приведенной ниже таблице, указаны диаметры сфер эквивалентных цилиндрам с различными значениями высоты. Значения последней строки таблицы наиболее типичны для больших частиц глины, имеющих форму диска. Может оказаться, что частица с диаметром 20мкм имеет толщину всего 0.2мкм. Как правило, мы не будем рассматривать такие примеры. Прибор, измеряющий объем частиц, может дать результат - около 5мкм. Поэтому, возникает возможность дискутировать на предмет точности результатов, получаемых различными методами анализа крупности частиц.

Обратите внимание, что при просеивании через сито с размером ячейки, например 25мкм, все эти цилиндры будут определены как частицы, размер которых < 25мкм. При анализе методом лазерной дифракции, эти цилиндры будут определены как частицы с разными размерами.

Размеры цилиндра		Отношение	Диаметр эквивалентной сферы
высота	диам.
20	20	1:1	22.9
40	20	2:1	28.8
100	20	5:1	39.1
200	20	10:1	49.3
400	20	20:1	62.1
10	20	0.5:1	18.2
4	20	0.2:1	13.4
2	20	0.1:1	10.6

Сравнение результатов, полученных различными методами.

Очевидно, если мы будем рассматривать нашу частицу под микроскопом, то мы смотрим на нее в плоскостной проекции, в которой можно измерить несколько ее диаметров. И каждый из этих диаметров характеризует эту частицу. Значения этих диаметров отличны друг от друга. Поэтому, важно понимать, что каждый метод определения размера частиц, основан на измерении различных характеристик частицы (максимальная длина, минимальная длина, объем, площадь поверхности и т.д.). Конечные результаты будут разными, в зависимости от применяемых методов, в каждом из которых применяется измерение разных физических характеристик частицы. Практически, можно сравнивать только результаты тех измерений, в которых один и тот же материал анализировался одним и тем же методом. Это, также, означает, что не может существовать стандартов и эталонов размеров для таких частиц, как зерна песка. Эталоном сравнения между разными методами анализа размеров частиц может служить только сфера. Однако, возможно использование стандартных эталонов сравнения для результатов, полученных разными приборами, но использующими один метод.

D[4,3] и т.д.

Представим три сферы, диаметр которых соответственно 1, 2 и 3 единицы. Какой средний диаметр этих сфер? Ответ - 2.00. Как  получен этот результат. Сумма значений всех диаметров

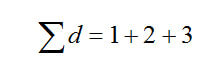
разделена на число частиц (n=3). Получаем среднее значение (более точно - среднее арифметическое значение длины), т.к. в уравнении фигурирует число частиц.

Среднее значение диаметра =

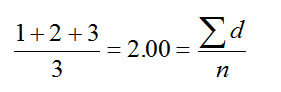
В математике это значение называется D [1,0], т.к. в числителе уравнения - значения диаметров, а в знаменателе - число частиц.

Для инженера по катализу наиболее полезным представляется сравнение этих сфер по значению площади удельной поверхности, т.к. чем больше площадь удельной поверхности, тем выше степень активности катализаторов.

Площадь поверхности сферы равна 4p r2. Поэтому для сравнения частиц по площади поверхности мы должны возвести значения диаметров в квадрат, разделить на число частиц и извлечь квадратный корень для того, чтобы вернуться к среднему арифметическому диаметру.

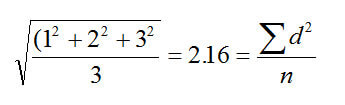
И снова это среднее арифметическое значение (приведенное к площади поверхности). Т.к. число частиц находится в знаменателе уравнения, а сумма квадратов диаметров в числителе то в математике это - D [2,0].

Для инженера химика, более актуальным будет сравнение сфер по их весу.

Вес сферы =

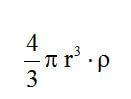
затем мы возводим значения диаметров в куб, делим на число частиц и извлекаем кубический корень, для того чтобы вернуться к среднему диаметру:

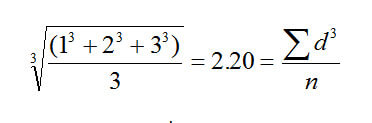
В данном случае мы получили среднее значение (среднее значение объема-веса), т.к. число частиц фигурирует в знаменателе уравнения. В математике это может быть представлено как D[3,0].

Вернемся к нашим частицам, которые имеют произвольную форму. Эквивалентная по объему нашей частице сфера в математическом виде это D[4,3], а сфера с эквивалентной площадью удельной поверхности  это D[3,2] или Sauter Mean Diameter (SMD). Эти значения рассчитываются следующим образом:

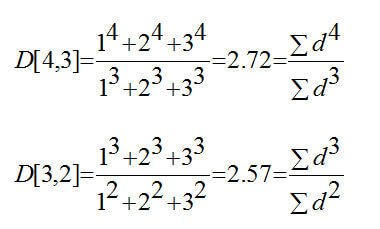
Обратите внимание на то, что число частиц (n) отсутствует, как в числителе, так и в знаменателе уравнения.

Метод анализа размеров частиц лазерной дифракцией, не требует знания количества частиц для получения среднего результата.

Различные методы анализа - разные средние значения.

При использовании электронной микроскопии, для получения среднего значения сумма размеров  частиц делится на их количество. Очевидно, что используя этот метод мы получим D[1,0] - среднее арифметическое значение длины. Имея систему обработки изображения, мы имеем возможность измерить площадь каждой частицы. Тем самым мы получим значение  D[2,0]. Если использовать прибор, работа которого основана на принципе электрозонной чувствительности, то мы сможем измерить объем каждой частицы, затем сумму значений объемов разделив на количество частиц, мы определим D[3,0].

Метод лазерной дифракции, на котором основана работа приборов серии Мастерсайзер, позволяет получать значение  D[4,3] или среднее значение  сферы с эквивалентным объемом. Это идентично среднему размеру сферы с эквивалентным весом, при условии, что плотность  - величина постоянная.

Итак, каждый метод анализа размеров частиц позволяет получать разные числовые значения средних диаметров, в зависимости от того какая характеризующая частицу величина является предметом измерения. Ниже приведены вычисления среднего диаметра трех сферы с диметрами 1, 2 и 3 единицы, и все ответы являются правильными.

Количественное и объемное распределение

Описываемый в данной главе упрощенный пример взят из статьи, опубликованной в журнале New Scientist (13.10.1991). В космическом пространстве на орбите Земли находится большое количество объектов. Ученые регулярно наблюдают за ними. Эти объекты классифицированы в группы по размерам.

Размер частиц  (см)	Кол-во частиц	% от общего кол-ва	% от общей массы
10-1000	7000	0.2	99.96
1-10	17500	0.5	0.03
0.1-1.0	3500000	99.3	0.01
Всего	3524500	100.00	100.00

Если мы рассмотрим третью колонку, приведенной выше таблицы, то сможем сделать правильный вывод - 99.3% всех частиц очень малы. Это процентное значение количественное распределение. Однако если мы рассмотрим четвертую колонку, то сможем сделать вывод (также правильный), что большинство частиц имеют размеры в диапазоне от 10 до 1000см. Т.е. частицы с такими размерами составляют почти 100% массы всех частиц представленной системы. Стоит отметить, что КОЛИЧЕСТВЕННОЕ и МАССОВОЕ распределение - это абсолютно разные значения, каждое из которых по своему характеризует систему.

И в этом случае, ни одно из распределений нельзя назвать не правильным. Объясняется это тем, что представленные исходные данные о системе были проанализированы разными, альтернативными путями. Например, при проектировании космического модуля, мы можем предположить, что легче защитить корпус модуля от попадания 7000 крупных объектов и это в итоге составит 99.96% массы от всей системы. Однако может оказаться более резонным предусмотреть защиту обшивки модуля от ударов мелких частичек, количественная доля которых составляет 99.3%?

С помощью калькулятора, мы можем рассчитать среднее значение описанных выше распределений и обнаружим, что среднее количественное значение составляет около 1.6 см., а среднее массовое значение около 500 см. Опять мы видим явное различие в полученных результатах.

Взаимные преобразования средних значений количества, максимальной длины и объема/массы.

Из предшествующих разделов мы знаем, что при измерении частицы на электронном микроскопе (разные методы дают разные средние значения), мы получаем D[1,0] - среднее значение диаметра по отношению к длине. Допустим, необходимо сделать перерасчет в среднее значение, приведенное к массе или к объему. Такое преобразование с математической точки зрения легко выполнимо, но мы подробнее рассмотрим возможные последствия подобных преобразований.

Подобный метод анализа размеров частиц на электронном микроскопе дает относительную ошибку ±3%. При преобразовании среднего количественного значения в среднее значение по массе мы используем кубическую функцию, и тогда наша ошибка также будет возведена в третью степень. А это уже ±27% относительной ошибки.

Однако, при анализе количественного или массового распределения методом лазерной дифракции, ситуация будет отлична от описанной выше. При анализе частиц находящихся в суспензии и при постоянной циркуляции этой суспензии через измерительную кювету, относительная ошибка будет не хуже ±0,5%. Если теперь преобразовать это среднее объемное значение в среднее количественное значение, то относительная ошибка составит менее 1%.

На практике, это означает, что при использовании электронного микроскопа и желании получить среднее значение объемного или массового распределения, эффект потери одной частицы с размером 10мкм будет равнозначен игнорированию одной тысячи частиц с размером 1мкм.

Поэтому важно сознавать "опасность" получения значительных ошибок при переводе значений одной системы в другую.

Программное обеспечение для всех приборов серии Microtrac работающее в среде Windows, позволяет вычислять многие производные диаметров, но использование этих результатов должно сопровождаться четким пониманием возможных погрешностей. Различные средние значения могут быть преобразованы в другие, при помощи следующих уравнений (преобразование Hatch-Choate) (Ref. 7).

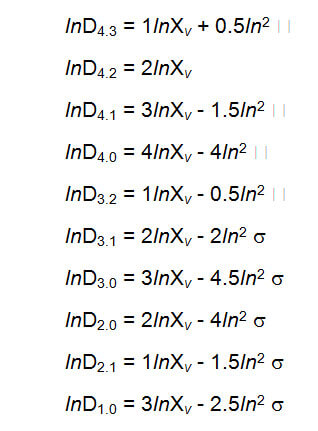
Измеряемые и вычисляемые диаметры.

Используемый фирмой Microtrac метод лазерной дифракции позволяет получать данные объемного распределения частиц по размерам по данным измеряемой индикатрисы светорассеяния. Полученные данные объемного распределения могут быть проконвертированы в значения количественного распределения или данные распределения частиц по макс. длине, как показано в предыдущей главе.

Однако, данные любого метода анализа использующего одну или другую теорию светорассеяния, должны с осторожностью и пониманием преобразовываться в другие данные распределения (смотрите главу Взаимные преобразования...). Пользователь должен четко представлять, какое распределение частиц измеряется непосредственно прибором, а какие рассчитываются посредством математических преобразований. Разные методы анализа размеров частиц будут давать разные результаты распределения, зависящие от фактически измеряемых параметров частиц.

Несомненно, большее доверие отдается измеряемым диаметрам, а не производным от них. На практике, в некоторых случаях, может оказаться “опасным” - строить окончательные выводы, основываясь на результатах полученных путем математических преобразований. Например, в итоговой таблице отчета об анализе программное обеспечение Microtrac показывает нам значение площади удельной поверхности в м2/см3 или в м2/г. Эти значения нельзя понимать как абсолютные и если пользователя интересует именно абсолютное значение площади удельной поверхности какого-либо материала, то для этого необходимо использовать метод и оборудование которые позволяют определять именно абсолютное значение площади удельной поверхности.

Какое значение мы используем.

Помните, что разные методы позволяют измерять различные характеристики (или размеры) нашей частицы и что полученные результаты мы можем различными способами привести к разным средним значениям (D [4,3], D [4,2] и т.д.). Какое же из всех  существующих значений мы должны использовать?

Простой пример - система состоящая из двух сфер с диаметрами соответственно 1 и 10 единиц. Представьте, что мы имеем дело с золотом. Если мы элементарно рассчитаем средний диаметр, то получим:

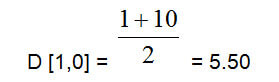
Итак, допустим, что средний диаметр частиц в нашей системе составляет 5.50 единиц. Однако мы должны помнить, что речь идет о частицах золота, но в первую очередь нас интересует вес материала.

Если у нас поточная линия, то нам неважно, что через нее прошло 3,5 миллиона частиц. Нас больше интересует, что вес золота равен, например 1 или 2 килограмм.

Зная, что среднее значение диаметра по массе это кубическая функция от диаметра, мы видим, что сфера с диаметром 1 единица имеет массу 1 единиц, а сфера с диаметром 10 ед. имеет массу 103=1000 единиц. В имеющейся системе частица  с  размером 10 единиц составляет 1000 частей из общих 1001 части по массе и, соответственно, мы можем пренебречь частицей имеющей размер 1 ед., т.к. в общем мы потеряем менее 0,1% от общей массы системы. Поэтому, среднее количественное значение не достаточно точно отражает отношение системы, где масса является доминирующей характеристикой. В данном примере больше других применимо значение D [4,3].

В нашем примере с двумя сферами среднее массовое (объемное) значение диаметров необходимо рассчитывать следующим образом:

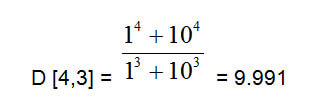
Это значение наиболее полно выражает нашу систему, где доминирующей характеристикой является масса и это значение также более значимо для технологов химического производства.

Другой пример. Представьте, что в сверхчистой комнате выращивают пластины кремния или арсенида галлия. В этом случае каждая частица попавшая на поверхность пластины может привести к появлению дефекта и очень актуальной становится информация о концентрации или количестве частиц в чистой комнате, т.к одна частица - это один дефект. Здесь предпочтительнее использовать метод прямого измерения количества частиц или метод измерения концентрации частиц.

Эти примеры наглядно демонстрируют разницу между измерением количества частиц и их размеров. Счетчики частиц, в отличие от анализаторов размеров частиц, позволяют регистрировать каждую частицу и производить их подсчет. Размер для нас, В последнем примере размеры частиц менее важны и необходимым может оказаться только количественный контроль частиц в ограниченных, интересующих нас диапазонах  размеров (например, до 8 классов).

При сортировке частиц по фракциям абсолютное их количество менее важно, чем их распределение по размерам. Для решения подобной задачи обычно требуется большее число диапазонов (классов). Для контроля правильной дозировки ингалятора, предназначенного для больных астмой, важны и концентрация (определяющая количество препарата) и распределение частиц по размерам.

Среднее значение, медиана и мода - основная статистика

Очень важно отличать эти термины друг от друга, т.к. очень часто они неправильно применяются как в математической статистике, так и в гранулометрическом анализе.

Среднее значение

Это некоторая средняя арифметическая величина, выражающая определенные характеристики. Существует несколько средних значений, которые могут применяться для характеризации размеров частиц.

Медиана

Это значение размера частиц, которое разделяет популяцию распределения точно на две равные  части, т.е. точка на кривой где 50% распределения находятся слева от этой точки, а 50% - справа. 

Мода

Модой, или модусом, называется такое значение размера частиц или класс распределения размеров, который в исследуемом распределении представлен в большем количестве, т.е. это наивысшая точка кривой распределения.

Представьте, что наше распределение - это нормальное распределение по Гауссу. В этом случае, среднее значение, медиана и мода будут расположены в одной точке (см. рис. 4).

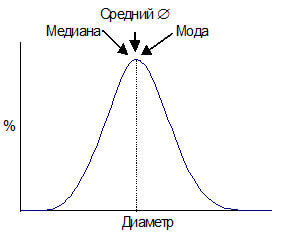
Рисунок 4.

А теперь, представьте бимодальное распределение, как показано на рис. 5.

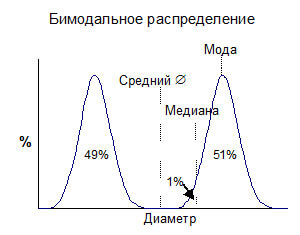
Рисунок 5.

В этом случае значение среднего размера частиц будет соответствовать точке кривой, которая расположена точно между двумя распределениям. Обратите внимание, что частиц с такими размерами очень мало, или возможно они вообще не представлены в распределении! Значение  медианы в нашем бимодальном распределении будет лежать в точке обозначенной на графике “1%”, т.к. именно эта точка делит распределение на две равные части. Мода в данном примере - это самая верхняя (по оси Y) точка кривой распределения, т.е. это частицы, которые представлены в наибольшем количестве в данной системе.

Этот пример наглядно иллюстрирует, что не всегда величина среднего значения, медианы и моды являются одним значением. Величина этих значений в большой степени  зависит от симметрии кривой распределения.

В таблице:

D[4,3]  объемный средний диаметр или иначе среднее значение De Broucker.

D[v,0.5] медиана объемного распределения, иногда показывается как D50 или D0.5.

D[3,2] средний диаметр по площади поверхности или Saulter Mean Diameter.

Различные методы анализа размеров частиц

Из предшествующих глав очевидно, что каждый метод дает разные результаты, т.к. разные методы измеряют различные параметры, характеризующие  наши частицы. Теперь мы обсудим некоторые преимущества и недостатки наиболее часто используемых на практике методов.

Ситовой метод

Это, пожалуй, самый старый из известных методов дисперсионного анализа, и основными его преимуществами являются дешевизна оборудования и возможность применения для грубодисперсных частиц, как например, в горно-перерабатывающей промышленности. В своей статье (ref. 2) Терренс Аллен обсуждает трудности получения воспроизводимых результатов при ситовом дисперсионном анализе. Далее приведены основные трудности и недостатки применения этого метода на практике:

• Ситовой дисперсионный анализ не позволяет исследовать эмульсии, а также дисперсионные системы, где дисперсионной средой является газ.
• Затруднен процесс измерения сухих порошкообразных материалов с частицами менее 400# (38мкм). Мокрый ситовой анализ частично решает эту проблему, но воспроизводимость получаемых результатов очень низка и выполнение такого анализа - задача достаточно трудная.
• Сложно измерять связанные и агломерированные материалы, например глины.
• Ситовой анализ таких материалов как TiO2 с размерами 0.3 мкм - просто невозможен. Этот метод не обладает высокой разрешающей способностью.
• Чем дольше продолжается анализ, тем более “занижается” точность конечного результата. Это происходит потому, что частицы имеющие чуть вытянутую или игольчатую форму, при продолжительном встряхивании ориентируются и проходят через сито. Поэтому стандарты, описывающие процедуры ситового анализа, должны очень строго регламентировать время измерения и способ управления движением (встряхивание или вибрация) сит.
• При ситовом анализе вытянутых или игольчатых частиц не воспроизводится истинное значение весового  распределения. Это может служить причиной получения противоречивых результатов при многократном анализе одного и того же образца (например, стержнеобразные частицы парацетамола в фармацевтической промышленности).
• Износ и допуск. Поинтересуйтесь таблицей размеров сит по любому из действующих в стране стандартов и сравните средние и максимальные допуски размеров отверстий, при которых сита еще разрешены к использованию.

Седиментационный метод

Седиментация - традиционный метод дисперсионного анализа, используемый в лакокрасочной промышленности, но результаты получаемые этим методом заведомо неточны (занижены). Этот метод эффективен только для достаточно узкого диапазона размеров частиц - от 2 до 15 мкм (Ref's. 1 и 2).

Скорость и время оседания частиц различного размера неодинаковы: более крупные частицы оседают быстрее. Это обстоятельство лежит в основе дисперсионного анализа методом седиментации. Для определения размеров частиц дисперсной фазы седиментационным методом разработано несколько типов приборов. В приборах с гравитационным полем, частицы дисперсной фазы в результате оседания накапливаются в специальной кювете, где фиксируется вес осадка частиц Q. За время t вес осадка достигает постоянного значения, и оседание прекращается. Опытным путем определяют кривую седиментации. Зная H (путь оседания частиц) и время оседания t, находят скорость оседания v = H/t. Далее с учетом этого несложно определить радиус частиц:

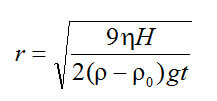
Оборудование для гранулометрического анализа методом седиментации может быть простым, как, например пипетка Андреансена, или более сложным - с использованием рентгеновского излучения, гравитационного или центробежного поля.

Более детальное исследование уравнения Стокса показывает, что у седиментационного метода есть некоторые недостатки, которые негативно сказываются на некоторых областях его применениях в качестве гранулометрического анализа.  Во-первых, необходимо знать плотность дисперсной фазы поэтому, этот метод неприменим для эмульсий, в которых дисперсионная фаза не оседает (седиментационно-устойчива). Также метод неприменим для систем, где дисперсная фаза имеет высокое значение r или состоит из смеси материалов различной плотности.

Конечный результат этого метода дисперсионного анализа - диаметр Стокса (DST), а это совсем не тоже самое, что D[4,3]. К тому же, конечный результат это некоторое значение, а именно радиус такой сферической частицы, которая седиментировала бы с той же скоростью, что и реальная частица в исследуемой системе.

Вязкость в приведенной формуле указывает, что необходим очень точный контроль температуры (термостатирование) при выполнении анализа, т.к. изменение температуры всего на 10 С влечет изменение вязкости приблизительно на 2%.

Элементарным расчетом можно вычислить, что частица SiO2 (r=2.5) с размером 1 мкм будет оседать через 1 см воды (при температуре 200 С) под силой гравитации в течение 3.5 часов.

Такой анализ требует много времени и проведение повторных экспериментов достаточно утомительно.

Для решения этой проблемы часто прибегают к увеличению значения "g" (приборы с гравитационным или центробежным полем).

Недостатки такого решения, т.е. увеличение значения "g", обсуждены в (Ref.3). В дополнительной литературе (Ref.2) можно найти более подробные аргументы, свидетель-ствующие о недостатках седиментационного метода для гранулометрического анализа.

Закон Стокса справедлив только для сферических частиц, и при условии, что в процессе оседания исключается столкновение частиц. Реальные частицы неправильной формы имеют большую удельную поверхность, чем идеальная сфера, и поэтому оседают медленнее из-за большего трения, чем сферические частицы с эквивалентными диаметрами.

Для частиц, имеющих форму диска, как например каолины, этот эффект выражается гораздо сильнее и заранее можно ожидать существенных отклонений конечных результатов от реальных.

Кроме того, при проведении анализа тонкодисперсных частиц седиментационным методом необходимо брать в расчет не только закон Стокса, но и Броуновское движение. Закон Стокса применим только к гравитационному осаждению частиц. В таблице на стр.8, приведено сравнение этих двух методов. Из нее видно, что седиментационный анализ частиц с размером менее 2 мкм дает ошибку которая может составить  около 20%. Для частиц с размером 0.5 мкм отклонение конечных результатов от истинных может составить до 100%.

Седиментационный метод заведомо дает заниженные размеры по сравнению с истинными, и поэтому многие производители, для которых важны абсолютные значения размеров частиц, получают недостоверную информацию.

В заключение отметим, какие основные недостатки имеет этот метод для производителей пигментов:

• Время дисперсионного анализа седиментационным методом длится в среднем от 25 минут до 1 часа, и это осложняет любой повторный анализ. С увеличением времени анализа увеличивается возможность агломерации материала.
• Седиментационный метод требует точной термостабили-зации измеряемой системы, т.к. температура сильно влияет на изменение одной из основных, участвующих в расчете конечного результата, величин - вязкости.

Electrozone Sensing (счетчик Культера)

Этот метод дисперсионного анализа был разработан в середине 50-ых годов для определения размеров клеток крови, которые являются практически мономодальной суспензией в разбавленном электролите.

Принцип работы таких приборов достаточно прост. Через калиброванное отверстие в стеклянном сосуде (трубке) протекает разбавленная суспензия и к ней прикладывается разность потенциалов . Емкость меняется в зависимости от размера частиц протекающих через отверстие. Изменение выражается пульсацией или появляющимся на мониторе пиком напряжения. В более старых приборах измерялась высота пика и эта величина сравнивалась с высотой пика стандартного латекса. Из этого следует, что это не прямой, а сравнительный метод и получаемые результаты не являются абсолютными. Корректировка результатов, связанная с ориентацией частиц, протекающих через луч, может осуществляться по значениям площади основания пика вместо значений высоты пика. Для клеток крови это прекрасный метод и в этом случае он может дать ответы не только о дисперсности, но и данные количественного распределения. Для реальных промышленных материалов таких например, как пигменты, существует ряд серьезных недостатков использования данного метода:

• Сложно анализировать эмульсии. Метод не позволяет исследовать дисперсионные системы где средой является газ! Следовательно, сухие порошкообразные материалы должны представляться для такого дисперсионного анализа только в суспензии. Т.е. прямой дисперсионный анализ сухих порошкообразных материалов - невозможен.
• Измерение необходимо выполнять обязательно в электролите. Затруднен анализ органических материалов, т.к. метод не позволяет измерять частицы в ксилоле, бутаноле и в других, плохопроводящих электри-ческий ток, растворах.
• Данный метод  требует использования стандартов для калибровки аппаратуры. Стандарты достаточно дороги и к тому же меняют свой размер в  дистиллированной воде и в электролите (Ref. 2).
• Метод медленный. Для материалов, имеющих относительно широкое  распределение (полидисперсное распределение), велика вероятность закупоривания маленьких отверстий частицами с относительно большими размерами.
• Нижняя граница размера анализируемых этим методом частиц, ограничивается величиной самого маленького отверстия, обычно не менее 2мкм. Отсюда вытекает невозможность измерения частиц TiO2 с размерами до 0.2 микрон.
• Материалы с высокой плотностью или частицы грубодисперсных материалов, не доходя до этапа протекания через отверстие, оседают на дно трубки.

В заключение, стоит отметить, что этот метод больше применим для исследования клеток крови, но не для дисперсионного анализа промышленных и индустриальных материалов.

Микроскопия

Оптическая микроскопия это метод, который позволяет оператору наблюдать действительные частицы, их размеры и форму. Поэтому этот метод позволяет решать, достигнута ли хорошая дисперсия и присутствуют ли в системе агломераты. Приборное обеспечение для оптической микроскопии сравнительно не дорого. Использование же достаточно дорогих электронных микроскопов, в сочетании с системами обработки изображения, позволяет анализировать химический состав фаз, а также с помощью современных программных средств обрабатывать сохраненное в электронном виде изображение. Однако интересно заметить, что 1 г. материала, состоящий из частиц размером 10 мкм и плотностью 2.5, содержит 760 x 106 частиц. При таком количестве частиц, невозможно  рассмотреть каждую частицу в отдельности. Случайные и систематические погрешности при использовании этого метода возникают из-за непредставительного пробоотбора, статистики подсчетов и ошибочной идентификации фаз оператором. Систематические ошибки из-за неправильной идентификации размера частиц обычно превышают погрешности статистики подсчета и приводят к тому, что у разных операторов при анализе одного материала получаются разные результаты. Все эти факторы говорят о невозможности использования оптической микроскопии в качестве метода для рутинного дисперсионного анализа в условиях производства.

Кроме того, если измеряется массовое распределение, то отклонения в результатах могут сильно возрасти - пропуск или игнорирование одной частицы  размером 10 мкм равнозначно потере или пропуску 1000 частиц с размером 1 мкм.

Электронная микроскопия требует сложной пробоподготовки  образцов, и поэтому, является достаточно медленным методом для дисперсионного анализа в условиях производства.

В оптическом микроскопе можно рассмотреть ограниченное количество частиц (в среднем 2000 частиц в день, при условии, что работает опытный оператор) и оператор достаточно быстро утомляется.

Опять же возникает проблема - "какой именно размер необходимо измерять?". Результаты исследований одного и того же образца, разными операторами, могут сильно отличаться друг от друга.

Однако, например для специалистов пигментного производства комбинирование микроскопии и лазерной дифракции, приносит неоценимую пользу.

Лазерная дифракция

Лазерная дифракция или более точно Low Angel Laser Light Scattering (LALLS) становится приоритетным стандартным методом определения дисперсности частиц во многих отраслях промышленности. Большинство лазерных дифракционных анализаторов позволяют определять дисперсность частиц в диапазоне от 0.1 до 2000 мкм.

Первые приборы, работа которых основывалась на этом принципе, были разработаны около 25-30 лет назад.

Фирма Microtrac выпускает серию приборов в основу работы, которых положен метод лазерной дифракции. Суть этого метода определения размеров частиц основывается на том, что регистрируются не сами частицы, а рассеянный свет от этих частиц (или дифракционная картинка) и угол рассеяния света универсально пропорционален размеру частиц.

Рассеянное частицами излучение регистрируется под разными углами с помощью высокочувствительного многоэлементного кремниевого детектора - фотодиодной матрицы. Излучение полупроводниковых лазеров с помощью линзы фокусируются в плоскость детектора, проходя при этом через измерительную кювету в которой осуществляется проток анализируемой суспензии, эмульсии или сухого порошкообразного материала.

При наличии в кювете частиц наблюдается рассеяние света (дифракция). Индикатрисса рассеяния (угловая зависимость интенсивности рассеянного излучения) определяется размером частиц и длиной волны лазера (последняя постоянна). Измерение индикатриссы и последующая программная обработка результатов позволяет за считанные минуты определить характер распределения частиц по размерам (дисперсионный состав) данной системы.

Фотодиодные матрицы обеспечивают одновременное измерение интенсивности рассеянного излучения.

Экспериментальные значения индикатриссы рассеяния получаются в результате усреднения данных о светорассении, регистрируемых через каждые 2 мс. Установив программно длительность анализа например 2 минуты, вы тем самым фактически выполните 6000 измерений. Ни один из традиционных методов дисперсионного анализа (седиментационный, ситовой или микроскопический) не позволят в такой короткий промежуток времени выполнить такое количество измерений! Кроме того, при исследовании, например суспензий и эмульсий, за две минуты все исследуемые частицы успевают пройти через измерительную кювету несколько раз, что обеспечивает получение устойчивых и в высокой степени воспроизводимых результатов. Огромным преимуществом такой скорости анализа, становится возможность не только контроля необходимой дисперсности материала, но и наблюдение в режиме реального времени за процессами агломерации и деагломерации!

Технология лазерного измерения размеров частиц была создана в начале 70-х годов прошлого столетия. С тех пор сменилось несколько поколений приборов, и современные модели позволяют решать любые задачи по анализу размеров частиц и отличаются высокой точностью анализа и легкостью в эксплуатации. Практически любые типы анализируемых материалов могут быть использованы благодаря широким методическим разработкам. Для работы с малыми количествами вещества используют автоматический малообъемный рециркулятор (ASVR), для автоматизации работы с большими сериями проб используют Автоподатчик (MAC-26).

Преимущества Лазерного анализатора Microtrac S3500 перед существующими аналогами:

Удобство настройки – самонастраивающаяся система, не требующая рутинных операций и специальной подготовки.

Высокая точность измерения – предусмотрен  автоматический расчет обратного рассеивания по теории Ми для сферических частиц и патентованный расчет Ми для частиц неправильной (игольчатой) формы. Поскольку реальные частицы чаще всего бывают неправильной формы, то эта уникальная особенность анализатора Microtrac S3500 особенно важна.

Разрешение - уникальная система трех лазеров в сочетании с оптическим мультидетектором позволяет получать разрешение высокой точности во всем рабочем диапазоне прибора.

Стабильность параметров – фиксированное положение лазеров и детекторов обеспечивает стабильные характеристики в течение длительного времени.

Возможность анализа в жидкой и сухой средах – прибор комплектуется устройствами ввода пробы в соответствующей среде, которые являются легко съемными и заменяются оператором в течении 2-ух минут.

Универсальность – модульная конструкция прибора позволяет заказчику приобретать его в конфигурации оптимальной для решения первоочередных задач, а затем расширить возможности прибора в зависимости от растущих потребностей и производственных задач. Данное преимущество позволяет подобрать для заказчика прибор с оптимальными характеристиками, что позволяет варьировать стоимость прибора в меньшую или большую сторону.

Автоматизация – прецизионная автоматика всех операций от пробоподготовки до анализа позволяет минимизировать возможные ошибки и погрешности.

Легкость и скорость калибровки – в приборе используется вспомогательный источник света для калибровки детекторов.

При выборе лазерного дифракционного анализатора дисперсности обязательно обратите внимание на то, по какой теории осуществляется анализ данных светорассеяния. В более старых, а также и в некоторых выпускаемых в настоящее время приборах других фирм, анализ осуществляется только по теории Фраунгофера, которая предполагает следующее:

• Размер частиц должен быть значительно больше длины волны используемого света (обычно около 5l, т.е. нижняя граница диапазона будет 3 мкм при использовании He-Ne лазера).
• Частицы различных размеров рассеивают свет с одинаковой интенсивностью.
• Частицы светонепроницаемы.

Использование теории с такими предположениями никогда не будет правильным для очень многих материалов, а для  высокодисперсных систем использование этой теории может стать причиной получения неправильных результатов, ошибка в которых может достигать 30% (например когда относительный показатель преломления частиц пигмента и  среды в которой они находятся, имеют близкие значения).

В средах и системах, состоящих из высокодисперсных частиц, где размер частиц приближается к значениям длины волны используемого света, рассеяние перестает быть прямолинейным (световая волна огибает частицы) и становится сложной функцией. Для решения такой задачи требуется уже другая теория - теория Ми.

Во всех перечисленных выше приборах серии Microtrac реализована как теория Фраунгофера так и теория Ми . В последней учтены все  условия взаимодействия света с частицами и средой. Такая комбинация теорий, применяемых в расчете конечных результатов, в одном приборе, позволяет обоснованно говорить о рабочем диапазоне такого прибора например от 0.02 до 3000 мкм.

Патентованная система трех лазеров обеспечивает высокую точность, широкий диапазон измерений и воспроизводимость результатов анализа.

Лазерные гранулометры Microtrac S3500, Nanotrac и Zetatrac позволяют получить достоверное представление о форме и размерах частиц методом лазерной дифракции и динамического рассеяния света. В субмикронном диапазоне отсутствуют отклонения между повторными анализами.

Стабильность и самонастройка системы основана на увеличенном числе лазеров, современной технологии обработки результата и использовании современных фоточувствительных датчиков.

Настройка работы этих приборов сводится только к автоматической юстировке (центровка) положения детектора, при котором на центральный сегмент детектора попадает максимум интенсивности излучения лазера (приборы использующие этот принцип не нуждаются в калибровке).

Принцип работы более старых и некоторых, существующих в настоящее время, приборов, основан на теории Фраунгофера, которая предполагает:

Размер анализируемой частицы больше чем используемая длина волны (обычно 5l  т.е. 3 микрона -  нижний предел при использова- нии He-Ne лазера).

Коэффициент рассеяния у всех частиц всех размеров одинаков.

Частица непрозрачна и не излучает свет.

Допустив эти предположения, легко убедиться, что они неприменимы к большинству материалов. А при анализе тонкодисперсного материала, особенно, когда относительный показатель преломления пигмента и среды почти одинаковы, возникает погрешность измерения,  достигающая  30%. Когда размер частицы приближается к длине волны света, тогда рассеяние становится сложной функцией с наличием  максимума и минимума.

В последних приборах фирмы Microtrac реализована полная теория Mie, позволяющая решать уравнения взаимодействия света с материей. Это позволяет проводить совершенно точные измерения в широком диапазоне. Теория Mie, в отличие от теории Фраунгофера  учитывает  объем частицы, а не расчетную поверхность.

Преимущества использования лазерной дифракции:

Метод основан исключительно на фундаментальных научных принципах. Следовательно, для проведения анализа абсолютно не требуется калибровка прибора по стандартным материалам. Прибор может быть сертифицирован на соответствие возможным существующим стандартам.  

Широкий динамический диапазон. Лучшее лазерное дифракционное оборудование позволяет пользователю измерять размеры частиц в диапазоне, например, от 0.02 до 2000 микрон. Частицы меньшего размера (1nm-1mm) могут измеряться посредством спектроскопии фотонной корреляции настолько долго, насколько они могут находиться в суспензии и не седиментировать.

Гибкость. К примеру, существует возможность измерять гранулометрический состав красок и лаков, распыляемых любого типа форсунками. В частности, это используется  разработчиками форсунок и пульверизаторов для достижения необходимого размера распыляемых частиц,  путем оптимизации вязкости,  P и размеров выпускных отверстий. Эта методика нашла широкое применение в сельскохозяйственной и фармацевтической промышленности.

В настоящее время, стандарт ASTM для контроля качества распыленных материалов предусматривает метод лазерной дифракции.

Возможно непосредственное, прямое измерение гранулометрического состава сухих порошков хотя  результат может быть получен при слабом   диспергировании их в жидкостях. Однако, в связи с анализом суспензий, это может быть ценно в плане оценки количества агломерированного материала, находящегося в сухой фазе.

Частицы, находящиеся в жидких суспензиях и эмульсиях могут измеряться при помощи циркулирования пробы через измерительную ячейку, что позволяет получать высокую воспроизводимость результатов. Измерение проб образцов. Несмотря на ничтожно малое количество, необходимого для анализа материала (4-10 г. для сухих проб, для суспензий обычно 1-2 г.) весь материал проходит через луч лазера и результат дифракции учитывается от каждой частицы. Поэтому, проба образца должна быть представительной.

Это неразрушающий  метод. Поэтому, дорогостоящие образцы  могут использоваться и после анализа.

Результат объемного распределения является прямым и при условии, что плотность постоянна, объемное распределение эквивалентно весовому распределению. А это то распределение, которое предпочитают знать инженеры химики.

Скорость получения результатов при использовании этого метода очень велика (около одной минуты).

Высокая воспроизводимость результатов этого метода. Это значит, что менеджер предприятия, путем сравнения результатов, может узнать что выпускаемый продукт изменился и, что изменение результатов не является причиной "приборного дрейфа".

Дифракция лазерного луча

Дифракция лазерного луча - это феномен, при котором лазерный луч, проходя через отверстие или встречая препятствие, распространяется и изменяет свое направление и интенсивность.

Когда лазерный луч пересекает узкое отверстие или проходит рядом с краем препятствия, он начинает "изгибаться" или расширяться вокруг краев, образуя характерную интерференционную картину. Это объясняется свойствами волновой природы света и явлением интерференции.

При дифракции лазерного луча образуется центральное светлое пятно, называемое дифракционным максимумом, окруженное темными и светлыми полосами, называемыми дифракционными минимумами. Распределение света в этой интерференционной картине зависит от размеров отверстия или препятствия, длины волны лазерного излучения и геометрии системы.

Дифракция лазерного луча имеет много практических применений. Например, в оптических системах дифракционные элементы, такие как дифракционные решетки, используются для разделения света на спектральные компоненты или для создания определенных интерференционных узоров. Это важно в спектроскопии, лазерной технологии, измерительной технике и других областях.

Дифракция лазерного луча также используется в голографии, где интерференционные узоры создают трехмерные изображения, и в оптической микроскопии для достижения более высокого разрешения и контрастности при наблюдении образцов.

Laboimpeks предлагает широкий спектр оптических компонентов, включая дифракционные элементы, для различных приложений и научных исследований, связанных с дифракцией лазерного луча. Наша компания предлагает качественное оборудование и профессиональную поддержку, чтобы помочь клиентам в их оптических проектах и экспериментах, связанных с дифракцией лазерного излучения.